Disk integration

Fundamental theorem
Limits of functions
Continuity
Mean value theorem

Differential calculus
Derivative Change of variables Implicit differentiation Taylor's theorem Related rates Rules and identities: Power rule, Product rule, Quotient rule, Chain rule

Integral calculus
Integral Lists of integrals Improper integrals Integration by: parts, disks, cylindrical shells, substitution, trigonometric substitution, partial fractions, changing order

Vector calculus
Gradient Divergence Curl Laplacian Gradient theorem Green's theorem Stokes' theorem Divergence theorem

Multivariable calculus
Matrix calculus Partial derivative Multiple integral Line integral Surface integral Volume integral Jacobian

Disk integration, (also known as Disc Method in Integral Calculus), is a means of calculating the volume of a solid of revolution of a solid-state material, when integrating along the axis of revolution. This method models the generated 3 dimensional shape as a "stack" of an infinite number of disks (of varying radius) of infinitesimal thickness. It is possible to use "washers" instead of "disks" (the washer method) to obtain "hollow" solids of revolutions, and uses the same principles that underlie disk integration.

Definition

Function of x

If the function to be revolved is a function of x, the following integral represents the volume of the solid of revolution:

$\pi \int_a^b {\left[R(x)\right]}^2\ \mathrm{d}x$

where R(x) is the distance between the function and the axis of rotation. This works only if the axis of rotation is horizontal (example: y = 3 or some other constant).

Function of y

If the function to be revolved is a function of y, the following integral will obtain the volume of the solid of revolution:

$\pi \int_c^d {\left[R(y)\right]}^2\ \mathrm{d}y$

where R(y) is the distance between the function and the axis of rotation. This works only if the axis of rotation is vertical (example: x = 4 or some other constant).

Washer method

To obtain a "hollow" solid of revolution (often called the "Washer method"), the procedure would be to take the volume of the inner solid of revolution and subtract it from the volume of the outer solid of revolution. This can be calculated in a single integral similar to the following:

$\pi \int_a^b \left({\left[R_O(x)\right]}^2 - {\left[R_I(x)\right]}^2\right) \mathrm{d}x$

where R_O(x) is the function that is farthest from the axis of rotation and R_I(x) is the function that is closest to the axis of rotation. One should take caution not to evaluate the square of the difference of the two functions, but to evaluate the difference of the squares of the two functions. ${\left[R_O(x)\right]}^2 - {\left[R_I(x)\right]}^2\ \not\equiv \; {\left[R_O(x) - R_I(x)\right]}^2$

NOTE: the above formula only works for revolutions about the x-axis.

To rotate about any horizontal axis, simply subtract from that axis each formula:

if $h$ is the value of a horizontal axis, then the volume =

$\pi \int_a^b \left({\left[h-R_O(x)\right]}^2 - {\left[h-R_I(x)\right]}^2\right) \mathrm{d}x.$

For example, to rotate the region between 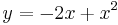$y=-2x%2Bx^2$ and $y=x$

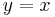
along the axis 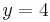$y=4$ , you would have to integrate as follows:

$\pi \int_0^3 \left({\left[4-\left(-2x%2Bx^2\right)\right]}^2 - {[4-x]}^2\right) \mathrm{d}x.$

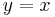The bounds of integration are the zeros of the first equation minus the second. Note that when you integrate along an axis other than the $x$ , the further axis may not be that obvious. In the previous example, even though $y=x$ is further up than 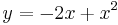$y=-2x%2Bx^2$ , it is the inner axis since it is closer to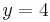 $y=4$

The same idea can be applied to both the y-axis and any other vertical axis. You simply must solve each equation for $x$ before you plug them into the integration formula.

References